Papers
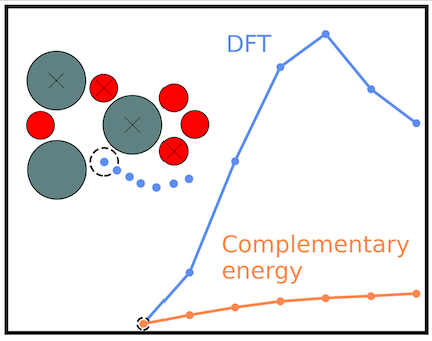
4.1 Complementary energy landscapes
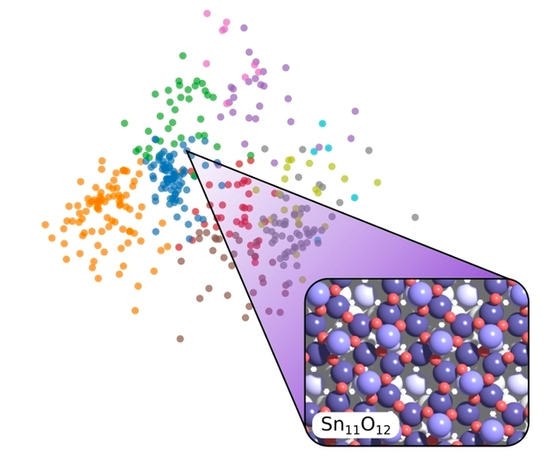
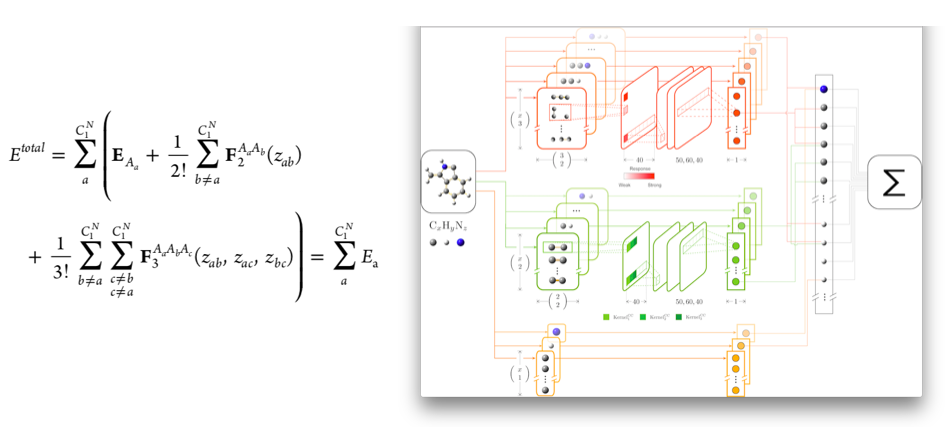
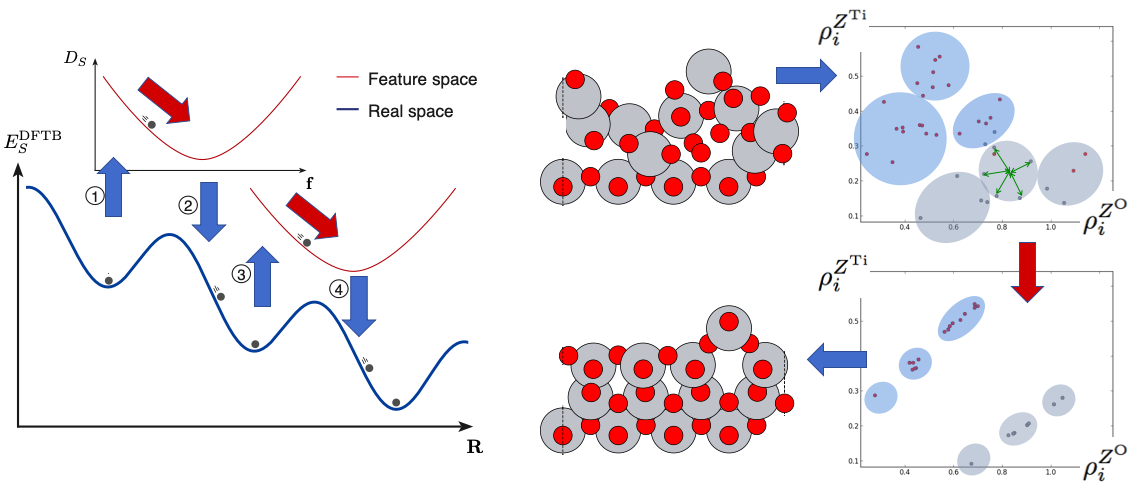
Stucture optimization in a corrugated energy landscape, such as DFT for atomic clusters and surfaces, suffers the presence of energy barriers between local minimum energy structures. In this work we propose to do the optimization in complementary energy landscapes, where some of the corrugation has been removed. We describe how the complementary energy landscapes may be constructed using various local environment descriptors, including SOAP, and different types of energy expressions. We demonstrate how the search for optimal structure proceeds faster in the CE landscape for a reduced SnO(110) surface reconstruction and for a silicate cluster, for which we find a hitherto unreported global minimum energy structure.
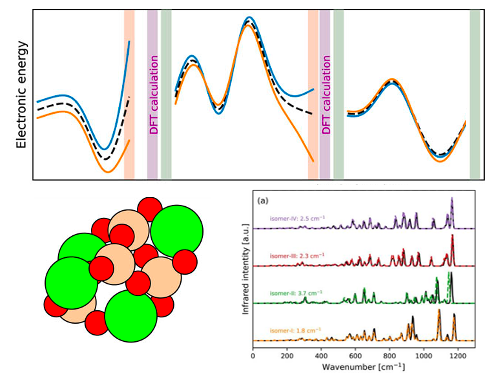
4.2 IR spectra with machine learning potential
We demonstrate that the combination of a Gaussian Moment Neural Network for energies and forces and a SchNet Neural Network for dipole moments can be trained to a reliable machine learning potential that can be used for calculating infrared vibrational spectra. The data acquisition relies initially on normal mode sampling and farthest point sampling. It is further augmented using an active learning protocol. Spectra are calculated for nanosilicate clusters and compared against full DFT-based molecular dynamics simulations.
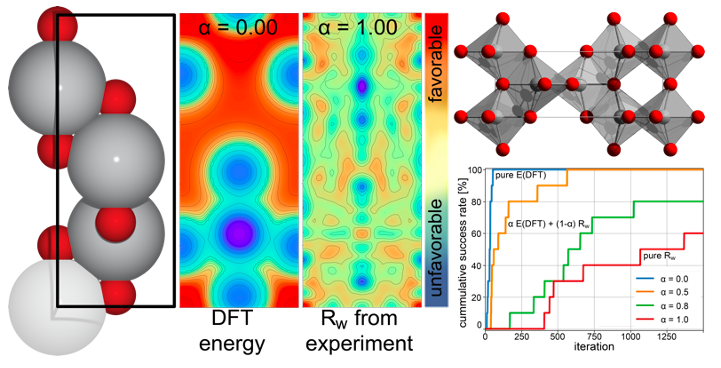
4.3 DFT+PDF object function
Determination of crystal structures of nanocrystalline compounds is a great challenge in solid state chemistry. Here, an algorithm is introduced that is able to determine the crystal structure of an unknown compound by means of an on-the-fly trained machine learning model that combines density functional calculations (DFT) with comparison of calculated and measured pair distribution functions (PDF) during the global optimization. The search in this combined DFT energy and PDF fit landscape can lead to the prediction of even metastable configurations and stacking disorder, which may not be found only relying on the thermodynamic stability at 0K, which is the case for searches only based on DFT energies.
4.4 local-GPR
In this paper we introduce a local descriptor, SOAP, and build a Gaussian Process Regression model based on that. The resulting GAP-like potential is used as the surrogate model for local relaxation in global optimization performed with the basin-hopping method.
4.5 AGOX
In this paper, we introduce our Python package for performing global optimization. The package supports a number of optimization methods, including random structure search, basin-hopping, evolutionary algorithm, and GOFEE.
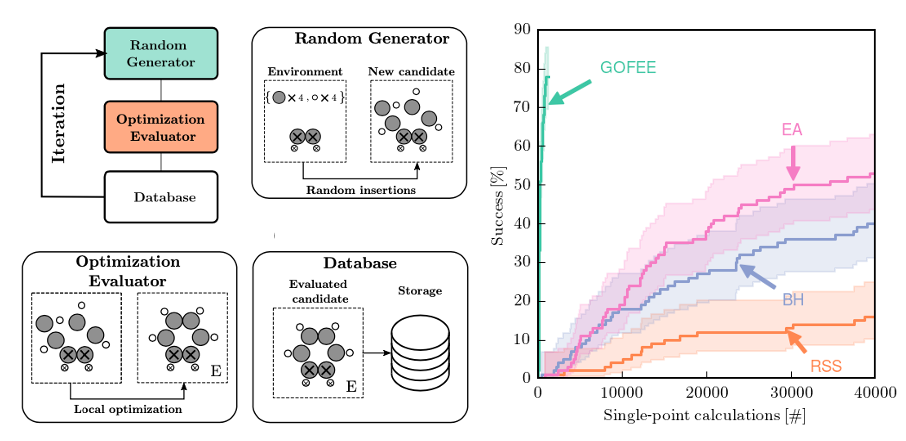
4.6 GOFEE-II
In this work, we provide a thorough analysis of the Global Optimization in First-principles Energy Expression (GOFEE) method. Many parameters are investigated and best practise in choosing their values is established.
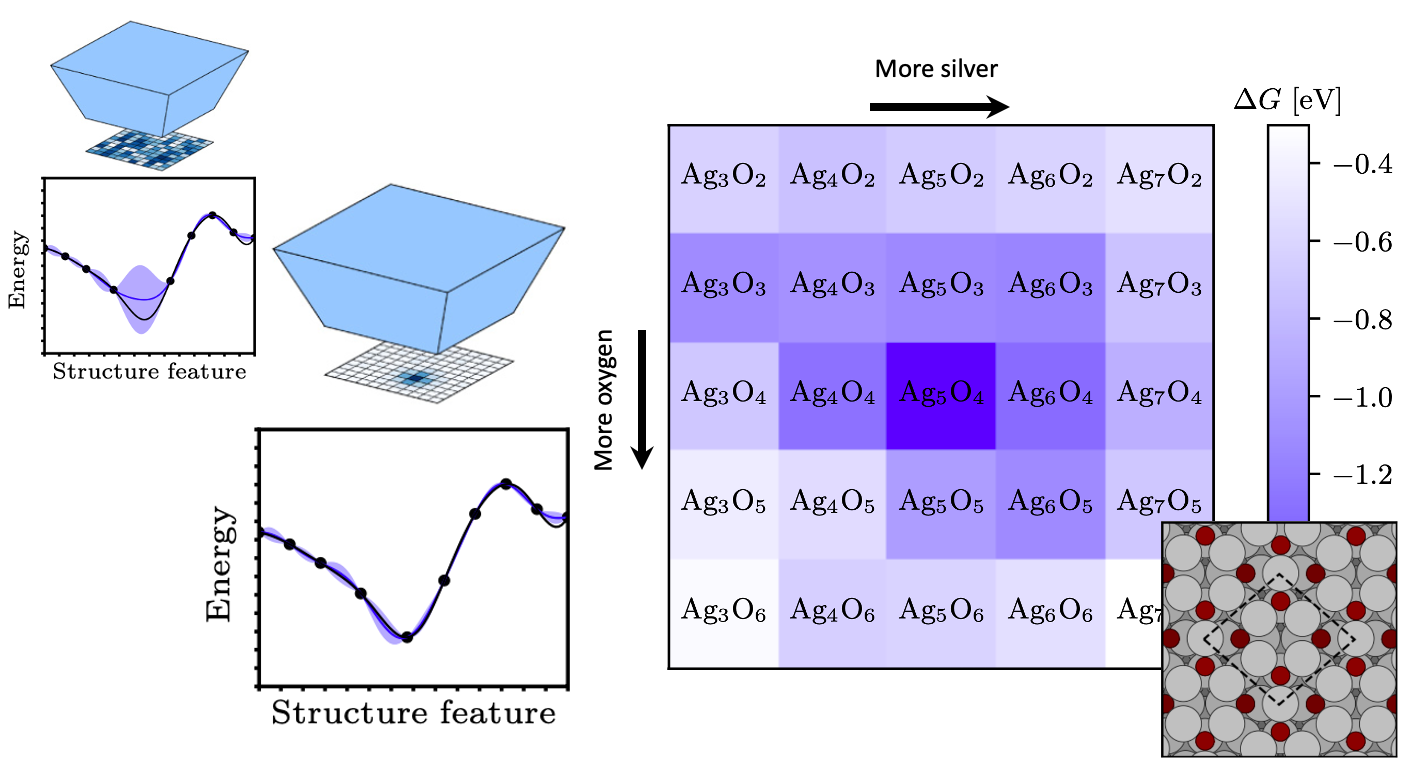
4.7 Ultra-thin oxide on PtSn(111)
A highly complex thin surface oxide of Sn on the surface of the PtSn(111) alloy is identified with experimental and computational means. The GOFEE approach is used, and the method is enhanced by introduction of a k-means based sampling technique.
4.9 ASLA-relax
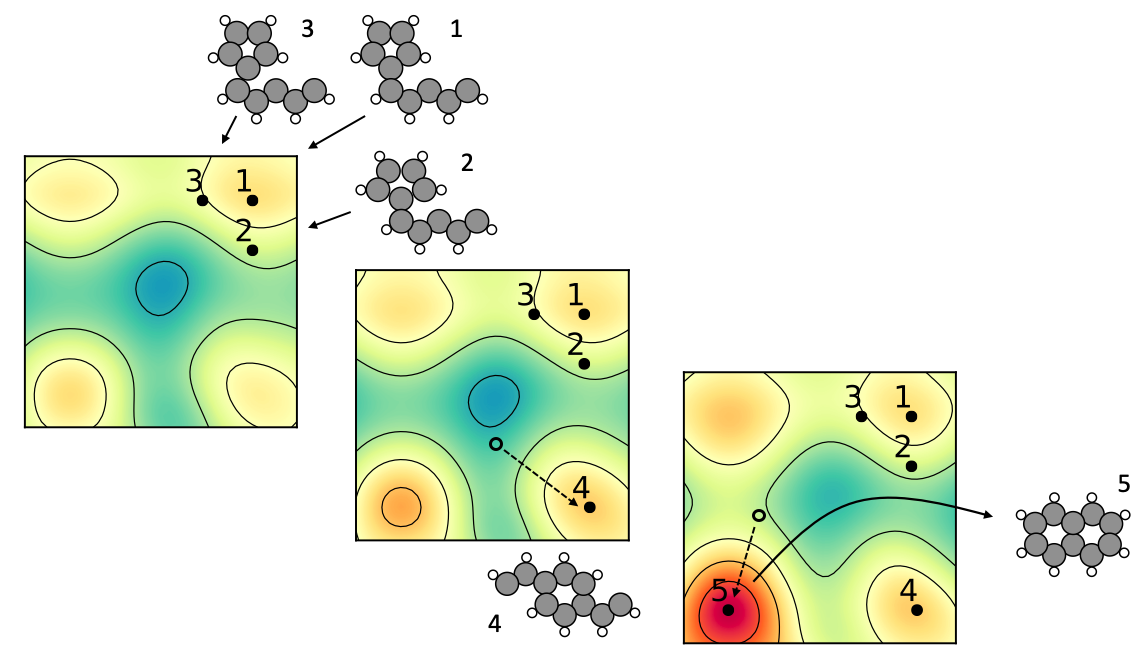
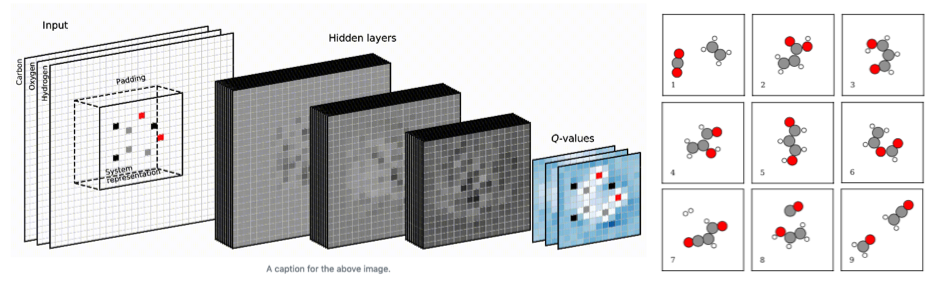
Using image recognition and reinforcement learning techniques, the ASLA method seeks to accumulate rational knowledge of how atoms bind in molecular complexes and solid state matter. The information is used in a self-guiding manner where new structures are built according to the gathered understanding (exploitation) and with some element of randomness (exploration). In this work we utilize a Gaussian Process Regression (GPR) method in addition to the neural networks (NN) of ASLA. The GPR is used to nudge structures built by the NN somewhat closer to local energy minima in the total energy landscape. Since the GPR requires less data than the NN, the combination of the two methods leads to a significant speedup, while the virtues of the orignial ASLA method are retained.
4.10 ASLA-representation
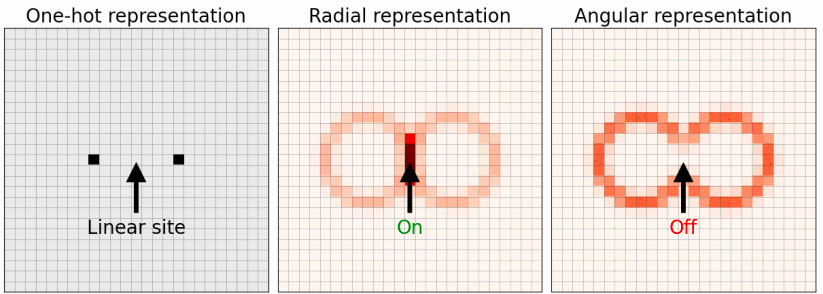
In this work, we investigate the importance of representation when molecular and solid state structures are identified via image recognition and reinforcement learning. In the original formulation, the ASLA method relies on a one-hot representation of the atoms. This means that image pixels at the center of atoms attain the value 1 while all other pixels have the value 0. As alternatives to this, atom-centered (Behler-Parrinello) Gaussian representations and the smooth overlap of atomic positions (SOAP) representation are obvious candidates. We find that the ASLA neural network is capable of identifying global minimum energy structures more easily with the Gaussian representation. Using the SOAP representation, the ASLA network may also gain efficiency, but the effect is too small to counter the delay caused by the network being presented with more input channels.
4.11 ASLA pseudo-3D
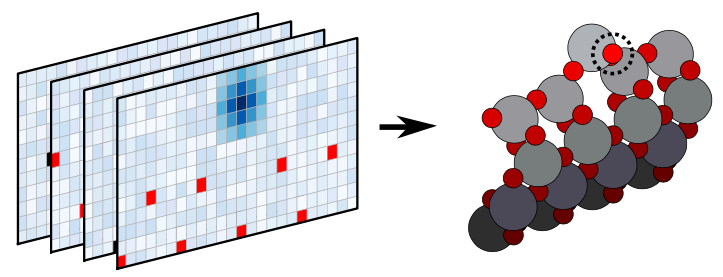
The recently proposed method ASLA combines image recognition and reinforcement learning and conducts automated structure search. In this work, we extend ASLA from two to three dimensions. The third dimension is handled as separate layers which are all treated according to the original 2D ASLA formulation. The versatility of the method is demonstrated through identificaion of the surface reconstruction of anatase TiO and rutile SnO surfaces.
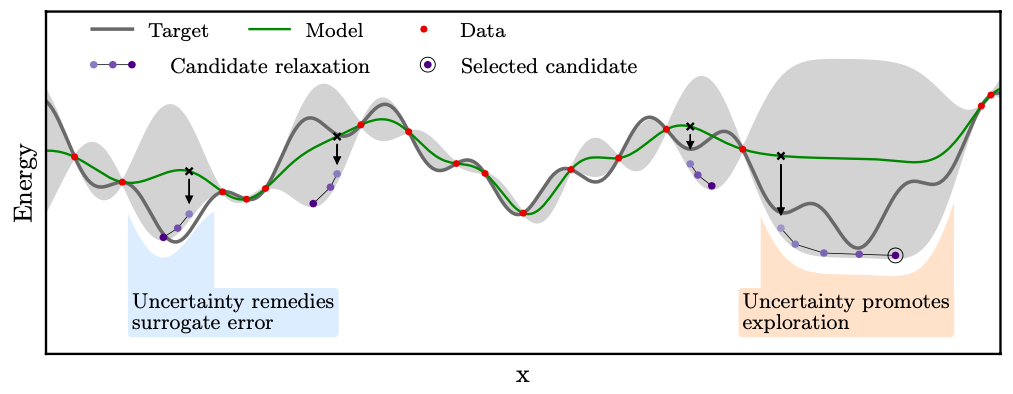
4.12 GOFEE
M. K. Bisbo and B. Hammer, PRL, 124, 086102 (2020)
Documentation and python code can be found here
Whenever global optimization of atomic structure is done with first-principles total energy methods, most of the computational effort is spent on evaluating the total energy. We propropose a scheme to actively learn a surrogate energy landscape while searching for a global minimum. By having several length scales in the surrogate model, we arrive at a method with high accuracy for predictions in both highly sampled regions and in regions of configurations that have not yet been visited. Using Bayesian statistics the most likely next configuration to investigate with the expensive first-principles method is sampled from a distribution of random and population-derived candidate structures.
4.13 Role model
S. Chiriki, M.-P. V. Christiansen, and B. Hammer, PRB 100, 235436 (2019)
The energy landscapes associated with the structural degrees of freedom for molecules, clusters, and crystaline materials contain many local energy minima. This renders the use of gradient-based optimization methods inefficient for global optimization. In this work, we propose that some of the gradient-based optimization be done in complementary energy landscapes, that are more convex than the true energy landscapes, yet share the position of global minimum energy structure. These complementary energy landscapes are constructed by measuring in a feature space the distance of atoms to some role model atoms they strieve to become like.
4.14 ASLA
Using image recognition and reinforcement learning, we let a neural network interact with a quantum mechanics solver (a density functional theory program). The network eventually trains itself into knowing the basic rules of organic and inorganic chemistry for planar compounds. After a few days of training on a few CPU cores, the network has taught itself to build a large number of sensible molecular and crystal structures.
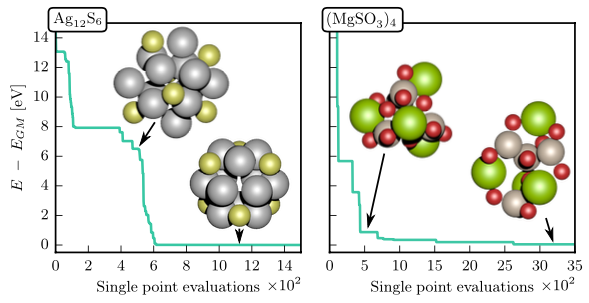
4.15 k-CON
Almost parameter free descriptor for neural network establishment of surrogate energy landscape (k-CON): Machine learning is often used to setup surrogate energy landscapes for molecules, clusters and solid surfaces. These are cheaply calculatable energy landscapes that attempt to mimic fully the true DFT energy landscapes. However, despite the name machine learning, it is often necessary for humans to design a proper descriptor for the entire structure or for each atom to compute the surrogate energy landscapes. It is unsatisfactory that humans have to prepare in depth part of the machine learning model with a lot of man made decisions on parameters. Hence we investigated if one could use the almost singular choice descriptor: all atom identities, all (reciprocal) distances for di-atoms, all sets of three (reciprocal) distances for tri-atoms, etc. as the descriptor. Used in conjunction with a neural network, it was shown that this is indeed possible and that the overall speed of an evolutionary search could be increased.
4.16 Autobag
Bundling of atomic energies as a means to divide the formation energy of a structure among its constituent atoms (auto-bag): With conventional methods (kernel ridge regression and neural networks) the extraction of local energies requires large amounts of data. As data is an expensive resource in connection with DFT calculations this subproject aimed at establishing bundled local energies so that atoms with similar local environments would have to share the same local energy. This method proves very robust in the limit of few available data points. It is anticipated to form the basis for improvement of other methods being developed in the VILLUM Investigator project.
4.17 Cluster regularization
Artificial energy landscape (i.e. not a surrogate energy landscape) for use in cross-over and mutation operations in evolutionary algorithm (cluster-regularization, role model search): Once structures are described by other means than Cartesian coordinates, new patterns in the atomic descriptors (features) reveal themselves. In this subproject, we discovered that if, for some crystal surface structure, the global minimum energy structure is known, it shows distinct clusters of local atomic environments. Now, for non-optimal structures, the sum of distances in feature space of all atoms to their nearest such cluster center correlates with the energy of the structure. This was flipped around and used in this way: clustering was imposed in feature space to non-optimal structures, hoping this would lead to the global optimization of energy versus structure.
4.18 LEA
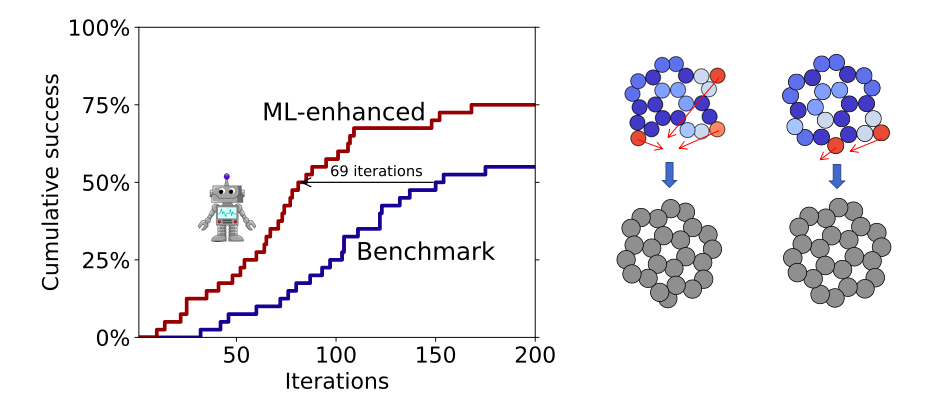
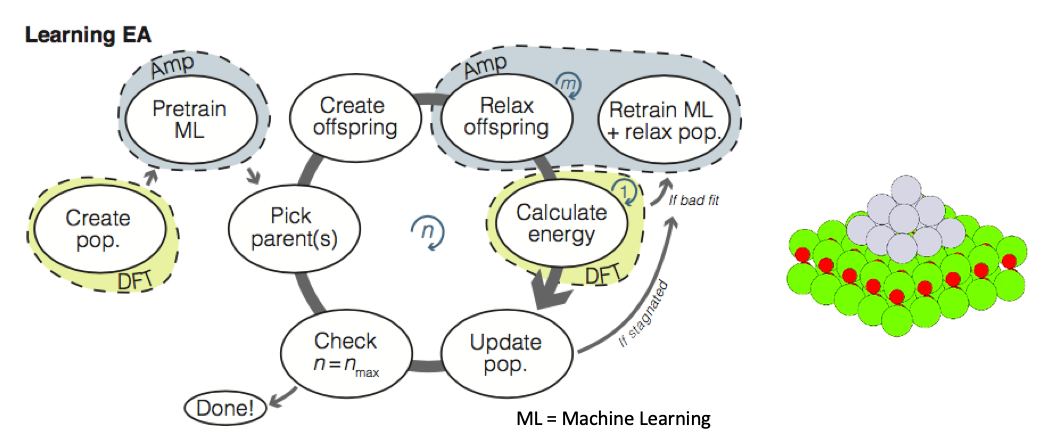
On-the-fly neural network establishment of surrogate energy landscape during evolutionary search (learning evolutionary algorithm = LEA): This project used an established neural network technology (Amp) to produce a surrogate energy landscape while an evolutionary structure search was carried out. Whenever the neural network and a single-point (=unrelaxed and hence cheap) DFT calculation disagree significantly on the stability of a structure, the neural network is re-trained. The project was carried out in collaboration with the author of the Amp method, Andrew Peterson, Brown University, Rhode Island, US. The speedup obtained allowed for more thorough searches and new exciting structures - never thought of by man - were discovered, including a hollow pyramidal Pt13 cluster on a magnesium oxide support.
4.19 TANGO
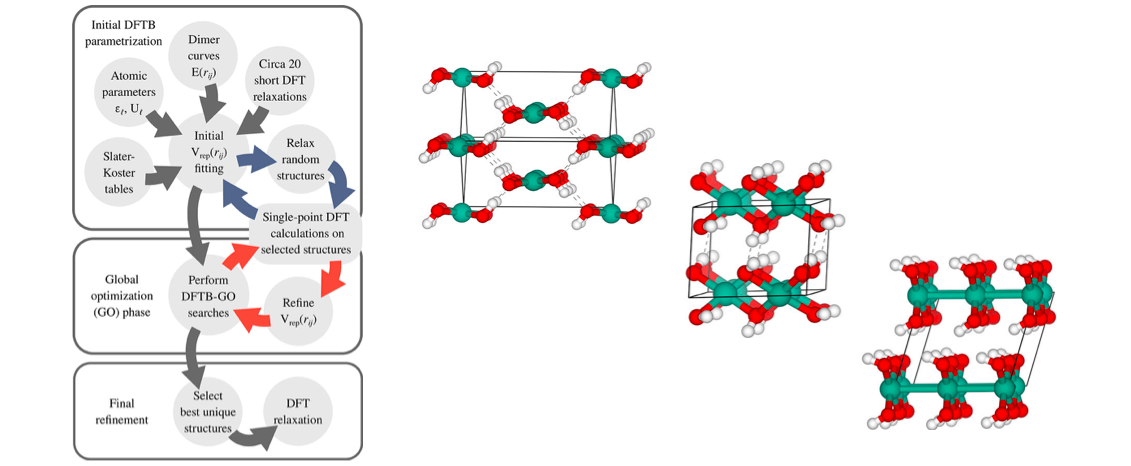
Performing global optimization with a full density functional theory (DFT) expression is computationally very costly as many relaxation steps must in general be done. Using e.g. an evolutionary approach, new structures originating from cross-over and mutation operations may require 50-100 such steps each implying many energy and force evaluations. In this work, we use the faster but more approximate density functional tight-binding method (DFTB) for the relaxation steps. In order to obtain near-DFT level of accuracy, we optimize some of the DFTB parameters on-the-fly by comparing to selected single-point DFT calculations.
4.20 Bayesian EA
M. S. Jørgensen, U. F. Larsen, K. W. Jacobsen, and B. Hammer, J. Phys. Chem. A 122, 1504-1509 (2018)
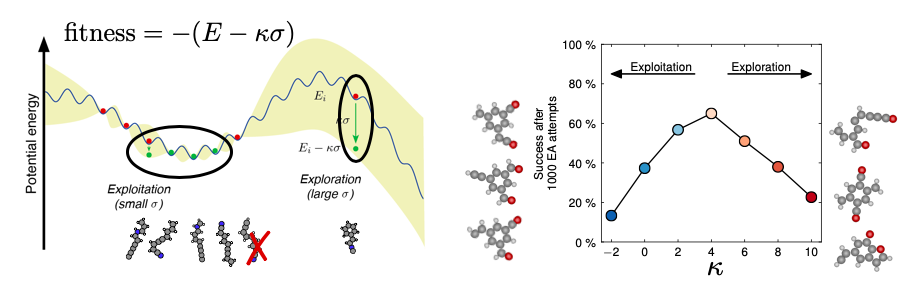
Parent selection in evolutionary algorithm: In this subproject, Bayesian optimization techniques are used to estimate the uncertainty by which the stability of a structure can be inferred from all other known structure/stability pairs. Parents are subsequently selected with a view at both stability (exploitation) and uncertainty (exploration). A paper was published with a volcano-plot showing a maximum in speed for an evolutionary search as a function of a single parameter.
4.21 On-the-fly
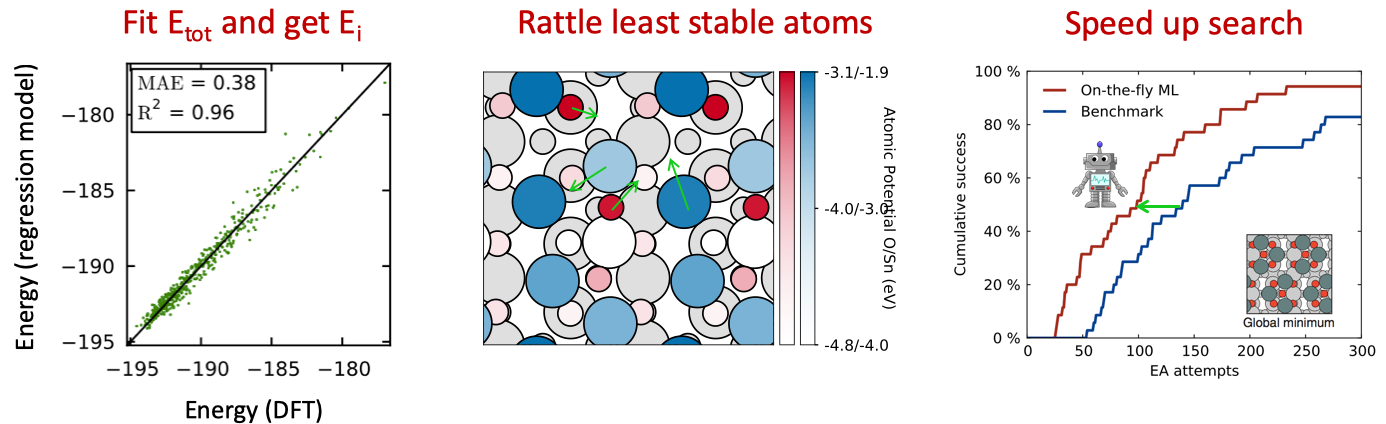
On-the-fly kernel ridge regression estimation of local potential energy during evolutionary search: When quantum mechanical calculations are performed (e.g. DFT calculations), a total energy is obtained for the entire structure and no information is available (or even well-defined) on how the individual atoms contribute to this energy. In this subproject, we investigated if a type of sensitivity analysis could reveal a clue about the potential of each atom in the final structure. Thus a kernel ridge regression model was used to estimate the energy cost of removing just one atom from a structure. The method works when applied to a small set of structures, where sometimes some atoms are detached from the others. This is the situation for evolutionary searches where the method proved successful. Was published in Phys. Rev. Lett. and is attracting quite a few citations.
4.22 Cluster EA
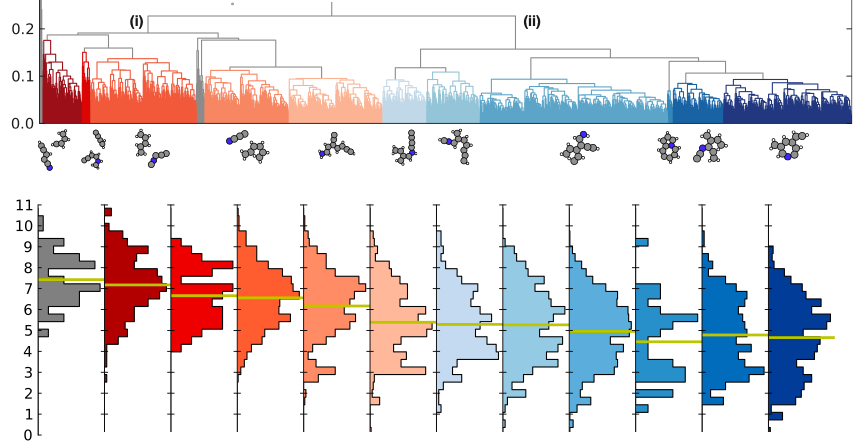
We introduce the unsupervised machine learning technique, clustering, to an evolutionary algorithm and thereby speed it up. The clustering technique allows us to label potential parent candidates in the population. It turns out that by more often using outlier candidates, i.e. the odd type parents, the evolutionary search for an optimal structure speeds up significantly.